ОПТИМАЛЬНЫЕ ОЦЕНКИ ФАЗОВЫХ КООРДИНАТ ЛИНЕЙНОГО ОБЪЕКТА

Закон управления линейным объектом (3.1) зависит от математического ожидания текущих значений фазо­вых координат объекта, определяемого при условии из­вестной реализации наблюдаемых величин г на предше­ствующем интервале времени (t0, t). Получаемые в ре­зультате значения обычно называют оценками фазовых координат и определяют по формулам, полученным Р. Калманом [9].

Рассмотрим вывод уравнений (3.1) для оценок коор­динат объекта, основанный на предположении нормаль­ности условного закона распределения координат x(t).

Пусть наблюдения вектора z.(t) производятся в ди­скретные моменты времени U, отстоящие друг от друга на время At, и в эти же моменты определяются оценки координат хи).

Обозначим

М [аг(^)| Zo=Xf (3.30)

На основании формулы Байеса

где kx — коэффициент, не зависящий от и определяе­мый из условия нормировки

| p(Xifzlo)dXi = . (3.32)

—00

Закон распределения величин г» при заданном ж* не зависит от прошлых значений ZtT1, так как я,- независи­мы, и может быть записан в виде многомерного нормаль­ного закона распределения величин я;:

PiZtlX;, *o-1) =7?(*,/*/)=

=£*expj —CiXif NTXzt-Сг*г]}, (3.33)

где Nt•

д t

Закон распределения величины Хі при наблюдениях величин zlo~1 = {z0, zlt… z^j) является априорным на шаге І. Предполагая его нормальным с математическим

ожиданием xai и дисперсионной матрицей/?<,», получим

р (xJziT1)^ exp j —і — [xt — ха1г R~l [х, — Я/]} •

(3.34)

Апостериорный закон распределения p(xt/zD — также

является нормальным с математическим ожиданием xz и дисперсионной матрицей Rt. Аналогично (3.34) имеем

p{xtz[)=kxexpj——— */]) . (3.35)

Здесь kx, kxa, kz — нормировочные коэффициенты, опре­деляемые из условий, аналогичных выражению (3.32).

Подставляя выражения (3.33), (3.34) и (3.35) в урав­нение (3.31) и приравнивая коэффициенты при одинако­вых степенях хі в левой и правой частях равенства, по­лучим уравнения

*t=[*7i+CjNflCt]-4tiNrlzt +R7ixet], (3.36) RT1=R7i—C]NT’Ci. (3.37)

В дискретном случае уравнение (3.1) объекта может быть записано в виде

Ч

— | [Bu(x)—%{x)]dx. (3.38)

4-і

Применяя к обеим частям уравнения (3.38) операцию условного математического ожидания при заданных зна­чениях гіГ1, получим при условии, что ы(т),

зависит только от гГ1 и не зависит от zit

Подставляя уравнение (3.39) и (3.38) в выражение для априорной дисперсионной матрицы, получим

Rai =[Е +7Ш] [Е + AbtY + $ (it) М, (3.40) где5(^) определяется из уравнения (3.2).

Подставляя уравнения (3.39) и (3.40) в выражения (3.36) и (3.37), получим

~ ^ 4

xi^[E+A^]xl-1+ f Budx+RtfNT’x ЧІ і

Rt=[E — RttfNT’Ci] {[£+ALt Rt-i [£+ Atd]T+

Рекуррентные соотношения (3.41) и (3.42) определя­ют оценки Хі и дисперсионную матрицу оценок /?/ в ди­скретном случае.

При М—получим уравнения для оценок фазовых координат объекта в виде (3.1) в непрерывном случае

=Ax + Bn + RCTN-‘[z{t)-Cx, (3.43)

dt

Начальными условиями этих уравнений являются ма­тематическое ожидание и дисперсия начальных значе­ний фазовых координат объекта х0. Заметим, что уравнения (3.43) и (3.44) остаются в силе, если матрицы А или С являются функциями управ­ления u(t). Это позволяет включить в рассматриваемые задачи случаи мультипликативных помех в канале пере­дачи команд u(t) и зависимости измерений z{t) от уп­равления u(t). Пример 3.2. Получим уравнения для оценок фазовых координат объекта = w — f — £ х (^о) = -*10 1 ^0 Х2 — Х -*2(*о) = -*20> I

J (3.47) I )

dx і /?іо л ~ — = « + -^(^“•*2); хг(і0) = М[х10];

dX О — Роп — — ИГ = Xi+ N (* ~ хд’ *2 (*°) = М t^ol-

Элементы дисперсионной матрицы определяются уравнениями

(3.48)

 

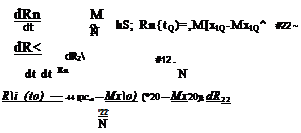і. 3. ОПТИМИЗАЦИЯ УПРАВЛЕНИЯ

ПРИ НЕФИКСИРОВАННОМ МОМЕНТЕ ВСТРЕЧИ

Предположим, что момент окончания процесса наве­дения (момент встречи /в) является случайным с изве­стной плотностью распределения p(tB). В этой задаче ма­тематическое ожидание в критерии

/ = М |г (О /> (*в) * (*0)+1+ f J (3-49)

означает операцию усреднения по начальным условиям x(to), возмущающим воздействиям n(t) и %(t) и момен­ту встречи tB.

Если величина tB не зависит от Хо, п, %, то (3.49) мож­но записать в виде

‘=Л4^||/?(/в)х

+ Ф-+. J P(QdtBf nJ, (3.50)

to to J

где интервал (to, T) включает возможные значения tB. Меняя порядок интегрирования во втором слагаемом и обозначая

Pi(Q=p(tB)P(tB <ь(*)=*п+лде|ж)<«., (3-si)

і

приведем исходную задачу к задаче минимизации инте­грального квадратического функционала вида ‘ г

/ =М К [хт (t) Рхх (/)+ ит (/)>! (t) и (О] dt I. (3.52)

Эта задача может быть решена на основе применения стохастического принципа максимума (гл. II) при FT*(*b)]=0 и

fQ(x, и, t)=xTP1x + uTQ1tt. (3.53)

Оптимальное управление по критерию (3.52) для объек­та (3.1) определяется из условия максимума функции

max Ж [/У (ф, х, и, t)gt*^=w. axM[ — xrP1x—

Сопряженная вектор-функция ф определяется в рас­сматриваемом случае дифференциальным уравнением

JL = _ Ат$ + 2Ргх (3.55)

при конечных условиях

Ф(Г)=0. (3.56)

Управление, максимизирующее уравнение (3.54) при положительно-определенной матрице еь определяется выражением

и{і)=±ь’ВтМ [ф(0иу • (3.57)

Оценка значения решения сопряженной системы урав­нений (3.55)

ф(*)=м[ф(0иУ (3.58)

может быть определена на основе метода фильтров Кал — мана.

Действительно, система п уравнений (3.55) вместе с системой (3.1) образуют систему 2п линейных дифферен­циальных уравнений

= — 4ГФ+2Р1х ♦(7’)=0;

at

-?±-=Ах+Ви—1; jf(/0)=jf0.

at

Эта система может быть записана в виде системы 2л. уравнений

М.=ау^Ьи+Ъ (3.60)

at

где

0

I

обозначают в блочном виде матрицы и векторы, состав­ленные из соответствующих векторов и матриц системы (3.59). Через 0 обозначены блоки, содержащие нулевые элементы.

-At$+2P1x + R. uCtN-1 (г-Сху, ф(Г)=0

dt

(3.61)

— ^Ax+Bu + R^CTN-1 (z-Cx); ;t(/0)=*0,

dt

где /?ф*, Rxx — дисперсионные матрицы оценок. Легко показать, что

-.♦(0=G W*. QW=0. (3.62)

Для этого подставим уравнения (3.62), (3.57) в (3.61) и заметим, что

Ri/X=QRXX. (3.63)

Полученная система уравнений может быть удовле­творена при произвольной х функцией Q(f), являющей­ся решением уравнения Риккати вида

*SL=2Px-A*Q-QA-±- QBq~1BtQ, (3.64)

Q(T)=0.

Таким образом, при нефиксированном моменте встре­чи управление, минимизирующее функционал (3.49), оп­ределяется выражением

u{t)=-jfiTlBTQx{tl (3.65)

где бі определяется выражением (3.51), Q является ре­шением (3.64), а х — оценка текущих значений фазовых координат объекта.

Пример. 3.3. Рассмотрим задачу управления объектом (3.20) при условии, что момент встречи распределен по равномерному закону в интервале (^о, 71), т. е.

1

Г —

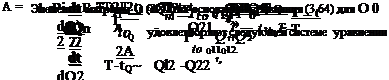Для критерия (3.21), одномерного управления и £>(/) = 1 из мат­рицы (3.22) и условия (3.56) получаем Д2 д

при конечных условиях Qn(T) =0.

Управление u(t) из уравнения (3.65) имеет вид

1

2ф4 Т — t

где Х и х2 определяются уравнениями (3.47).

3.4. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

ПРИ ЖЕСТКОМ ОГРАНИЧЕНИИ

Рассмотрим случай, когда управление линейным объектом с уравнением (3.1)

— = Ах— Ви ~(“І5 (3.66)

dt

не должно в каждой реализации превосходить заданных значений U(t), например, для скалярного управления

I u{t)<U{t £/>0. (3.67)

Ограничение (3.67) в дальнейшем будем называть жестким ограничением. Физически это условие отражает наличие в системе нелинейного элемента типа ограниче­ния.

нимизирующего квадратическую форму значений фазо­вых координат в момент встречи:

I=*M[xT{tu)Px{tu). (3.68)

Управление осуществляется, как и ранее, на основе измерения вектора z, определяемого выражением (3.3). В этой задаче

	Н(х, ф, и, ^)=фг[4л:-|-Ди+1].	(3.69)
где	d±=-A^, ф(д=~2/>*(д. dt	(3.70)
Управление определяется условием
	max М Н (дг, ф, и, Ц z** =0. ИОІ<Ц <oJ	(3.71)
Отсюда и	максимизирует величину фт Ви и равно
	n{t)—V (f) sign 2Гф (^),	(3.72)
где B(t)- А	-вектор (#Х1); ф(#)—вектор—(/гХ 1) при
Brijp(t) не равном нулю.
При		(3. 73)

управление не определяется из условия (3.71) и являет­ся особым по терминологии, принятой в детерминиро­ванных задачах.

Для определения оценок ф(/) и x{t) аналогично

(3.61) получаем систему уравнений:

£}=-a4+R**CtN-*(z-Cx), Ф(У=

at

= -2 Рх(іл), (3.74)

А л д

— = Ах+Ви+Яхх СгЛГ-і (г _ Сх)

dt

■*(*о)=*о-

Здесь х и Rxx — дисперсионные матрицы оценок, опре­деляемые уравнением Риккати типа (3.44), и управление u(t) определяется выражением (3.72).

Прежде всего отметим, что решение уравнения (3.70) имеет вид

* (3.75)

где кт(tB, t) — матрица импульсных переходных функций, являющаяся решением матричного уравнения

dkT^Bj)=-ATkr(iB, t), kT(iB, iB)=E. (3.76)

Таким образом, из выражений (3.72) и (3.75)

u(t)=-U(t)signBTkT(t„t)P(tB)M [*№;.] (3.77)

оптимальное управление в каждый момент времени t і максимально по величине и совпадает по знаку с оцен­кой конечного значения фазовых координат объекта при наблюдениях до момента t.

Однако управление в виде выражения (3.77) не мо — ! жет быть непосредственно реализовано, поскольку оно требует оценки будущих значений фазовых координат, зависящих согласно уравнению (3.13) от будущих зна­чений управляющего воздействия. Для определения за­кона управления в функции оценок текущих значений

фазовых координат x(t) будем искать решение системы

(3.74) относительно ф(0 в виде

Ф(*)=-<?{К, І) [х(І)+Ь(/)], (3.78)

I где матрица Q и вектор функция Ь (nXl), не зависят от ф и х.

Подставляя выражение (3.78) в уравнения (3.74) и S замечая, что

Rtyx== QR хх ■> (3.79)

получим дифференциальное уравнение

[^+ЄЛ+Лг<?]р^)+&(о] +

і 4&+B7/signir5,(*)j=0, (3.80)

1

При произвольном значении оценки х получаем

+ (3.-82)

dt

Отсюда для конечных условий (3.81) получим

Q{t„t)=2kT{tB, t)P{Qk{t„t (3.83)

где kT{tR, t) удовлетворяет уравнению (3.76), а k(tv /^ — транспонированному уравнению.

При

BT§{f)> 0 (3.84)

вектор b(t) удовлетворяет уравнению

— — Ab + BU=0, где &(/в)=0 (3.85)

dt

И

‘в

b{t)~ J k(t, т)BUdr; (3. 86)

t

при

BTi{t)< 0 (3.87)

имеем

-—Ab-BU=0, b(tB)=0 (3.88)

dt

и

b(t)—— J k(^, t)BUdr. (3.89)

t

Подставляя в соотношения (3.84) и (3.85) выражения (3.79), (3.86) и (3.89), получим неравенства

л. V

BTQx <-BTQ k(t, r) BU dr; (3. 90)

t

л Г

BTQ v > k (t, t) BU dr. (3. 91)

Из этих неравенств при

*•

BTQ j k (t, x) BU rfr > 0 (3.92)

t

следует, что в области существования решения (3.72)

Л гв

BTQx | > | BTQ k {t, т) BU dr I (3. 93)

t

и, следовательно,

BTQx[>BTQb. (3.94)

Таким образом, при Вт^{і) ФО

u(t)=-U (t) sign ВЧТ(*в, /) Р(О £ (/в0 дг (/) (3. 95)

и решение пропорционально знаку оценки текущих зна­чений фазовых координат.

Пример. 3.4. Рассмотрим задачу определения управления

М<1

линейным объектом

XI = И + С, Х (^о) = -*10» ■*2 = *I. X2(tQ) = X2Q

по критерию минимума среднего квадрата пролета Я = Д.*і(*в) + .*2 (*в)- В рассматриваемом случае

Д2 Д Д 1

Произведение матриц

BTkr(tB, t)P(tB)k(tB, t) X(і) = (tB + b~t)[(ів + Д — t)X (t) +

+ *2(0]*

так как

t<tB, Д>0, то

и (О = sign [(*в + Д — 0 Xi(t) + х2 У)],

Непосредственной подстановкой можно показать, что ‘в

BTQ{tt) J k(t, x)Bdx = 2(tB + 2/i — ()>Q.

t

поэтому условие (3.92) выполняется.